Big O for Beginners

Big O notation is one of the most ubiquitous pieces of mathematics in computer science. Being aware of Big O notation and program time complexity can make you a better programmer. But what is it, and why is it useful?

How Do We Compare the Relative Performance of Algorithms?

Tom Scott has a great introduction to his experience with runtime complexity and Big O notation. Take a watch!

What is Big O Notation?

Big O notation is a mathematical way to roughly compare how different algorithms will perform as the size of the input n increases.

The n in our Big O notation can mean different things based on the context. For algorithms, it usually refers to the size of the input. Here are some examples:

• If we are making a sorting algorithm, our n is the number of elements our algorithm needs to sort.
• If we are making a search algorithm, our n is the number of elements in the collection that we are searching over.
• If we are making an algorithm to find the best path across a road network, our 'n' might be the number of intersections in the road network.¹

By understanding how the time it takes for different algorithms to run increases with the input size, we can be more selective in the ways we solve problems and ultimately write faster and more efficient code.

Practical Example: Searching for an Enemy in the Scene

Say we are making a game with enemies, and we need a fast way to find an enemy given some integer ID.

GameObject.Find()

An obvious way to solve this problem is by using GameObject.Find(). If we name each enemy GameObject by its enemy ID, we can use GameObject.Find() to

According to the Unity documentation, GameObject.Find does what is called a linear search over every GameObject in the scene to find the object in question. This means that the search algorithm behind GameObject.Find() looks something like this:

public static GameObject Find(string name)
{
    // For every game object in the scene...
    foreach(GameObject gameObject in [THE LIST OF OBJECTS IN THE SCENE])
    {
        // If this current object is the object we are looking for...
        if (gameObject.name == name)
        {
            return gameObject; // return it
        }
    }

    // If we go through every object and 
    return null;
}

Another way to think about a linear search is thinking about how one would look through an unsorted deck of cards for a particular card. To find a card in a scrambled deck, you have to lift each card one-by-one and check if that card is the one you are looking for. We can say that in the best case, the first card you pick up is the one you are looking for. So, in the best case, a linear search is O(1). However, imagine you are looking for a card that isn't even in the deck. You would have to look through every single card in the deck to come to finally find that card.

If we imagine the deck being of some arbitrary size n, we could say that in the worst case, it would take O(n) operations to find the card. That means if the deck was size n, you would have to pick up and check n cards.

With this thinking, we can get a good idea for how using GameObject.Find might impact our game's performance. In our case, n is the number of objects in the scene. This means that the more objects we have in the scene, the longer it will take for our enemy lookups to find the desired enemy. This might work for a game with less than 100 GameObjects in our scene, but things might quickly slow down if we have complex scenes with many thousands of GameObjects - especially on slower machines.

But is there a better way?

Using a Hashtable (Or Dictionary<K, V> in C#)

A hashtable is a data structure that is an array that organizes its elements based on a value called a key. The key is used to calculate an index for the value to store. The idea is that if you have the key, you can do a quick calculation to know exactly what index the given value should occupy. This calculation requires the same amount of time no matter how big the underlying array is.

The first five minutes of the following video gives a very great overview of how hashtables are able to look up elements in a list very quickly.

So, we could use a hashtable to store our enemies in our game by their ID. The ID is the key, and the corresponding enemy GameObject is the value stored.

So, we could create a class EnemyManager that has a hashtable of the current enemies in the game organized by their ID, and each enemy could have a component EnemyController that adds their GameObject to the EnemyManager's hashtable of enemies. Then, we only need to call a hashtable lookup function to see whether there exists an enemy of a given ID.

In C#, the System.Collections.Generic namespace already has a finished hashtable class we can use; it's (somewhat confusingly for beginners) called the Dictionary. We don't even have to implement the hashtable ourselves; we can just use the one in the .NET Framework!

How this would look like in code is as follows:

// EnemyManager.cs -- On some manager gameobject.
public class EnemyManager : MonoBehaviour
{
    private Dictionary<int, GameObject> enemiesById = new Dictionary<int, GameObject>();

    public void AddEnemyToDictionary(int id, GameObject go)
    {
        enemiesById.Add(id, go);
    }

    public void GetEnemyById(int id)
    {
        // This is an O(1) operation; no matter how
        // many enemies are in the dictionary, calculating
        // the position of the enemy in the table based on its
        // id will take the same amount of time. This means that
        // this will run fast no matter how many enemies there are.
        // There could be millions; it wouldn't matter!
        if (enemiesById.Contains(id))
        {
            return enemiesById[id];
        }
    }
}

// EnemyController.cs -- On every gameobject.
public class EnemyController : MonoBehaviour
{
    public EnemyManager manager; // Assigned in inspector
    public int id;

    private void Start()
    {
        manager.AddEnemyToDictionary(id, gameObject);
    }
}

Because this method uses a hashtable, which takes the same amount of time to lookup an enemy based on an ID no matter how many enemies are in the table, we can say that this algorithm is O(1), or 'constant' time complexity. No matter the value of 'n', it's going to take the same amount of time to find an enemy. We could have millions of enemies, and it wouldn't matter!

How Much Faster is the Hashtable?

If we graph our Big O functions, we can get a good visual for how much faster the dictionary is over the

!

As we can see, the difference is dramatic. The larger n gets, the better the dictionary is in comparison to GameObject.Find().

Data Structures and Big O Notation

From our case study, we can see that just a basic understanding of Big O notation can inform what data structures and approaches we use to solve particular problems in the fastest way possible.

Finding the Big O time complexity of common data structures and algorithms is fairly easy; just look it up. Below, you can find a cheat sheet for the Big O runtimes of common data structures and their operations:

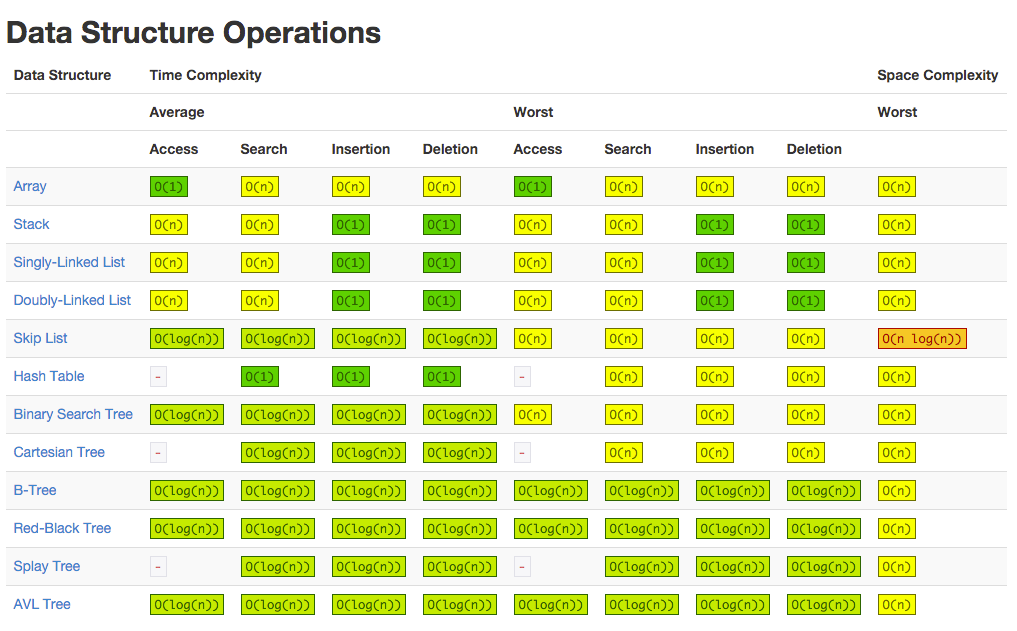
For example, if I was making a program where I had to add and remove elements from a collection very frequently, I could look at this table to find a data structure that has good runtime performance for insertions and deletions. The LinkedList looks like a good candidate; it has O(1) insertions and deletions.

Comparison of Common Big O Functions

The following graph shows different Big O functions and how the time it takes to process an input varies with the size of the input.

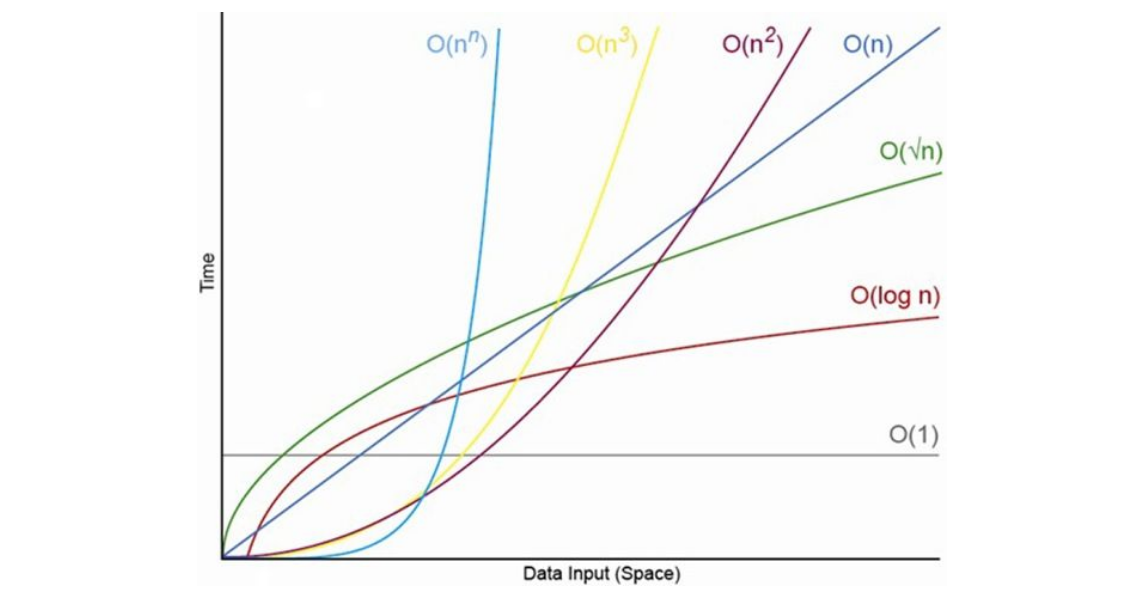
Here are some examples of different problems that fit certain Big O time complexities:

• O(1): Accessing an array by its index.
• O(n): Looking for a particular value in an array using a linear search
• O(n log n): Sorting an array using a divide-and-conquer algorithm like MergeSort.
• O(n^2): Printing all possible ordered pairs (a, b) of an array.
• O(2^n): The Travelling Salesman Problem

Conclusion

Big O notation is a huge part of computer science. If you choose to major in Computer Science, you will find that calculating the Big O runtime of your algorithms is an important skill. Hopefully, with a new basic understanding of Big O notation, you should be equipped with the knowledge necessary to make informed decisions about which data structures to consider for solving various programming problems.

---

1. For problems that have more complex inputs such as pathfinding, we often express our Big O notation in terms of multiple variables. Pathfinding is a graph theory problem, so we express our Big O notation in terms of N, the number of nodes (in this case, intersections in the road network), and E, the number of roads in the road network. ↩